人体成分分析报告可信度有多少 如何评价我的体测表  在做主成分分析（pca）时，选取的主特征是原来数据的哪些特征呢

明天我们将要学习R言语进阶中*重要的统计内容---主成分剖析，它在我们的研讨中简直是无处不在，运用*广的就是将主成分放入回归模型停止拟合，用于矫正相关的混杂要素。

主成分剖析的基本思想是将多个变量停止线性组合，在保管原数据主要特征的同时增加变量个数，从而到达降维的目的。R言语的内置函数princomp提供了未经旋转的主成分剖析。

1. 惯例主成分剖析

在这里，我还将以鸢尾花数据集（iris）为例引见如何在R中停止主成分剖析：

# 主成分剖析
# 输入原始数据并提取相关主成分
mydata <- iris # 将iris命名成mydata以便后续操作
mydata$type[which(mydata$Species== "setosa")]<- 0 # 设置setosa为0
mydata$type[which(mydata$Species== "versicolor")]<- 1 # 设置versicolor为1
mydata$type[which(mydata$Species== "virginica")]<- 2 # 设置virginica为2
attach(mydata) # 固定数据框
fit <- princomp(~ Sepal.Length+Sepal.Width+Petal.Length+Petal.Width, cor=TRUE) # 对花萼和花瓣的相关数据停止主成分剖析，cor=TRUE表示从相关系数矩阵提取主成分（实践上是对数据的一种规范化）
summary(fit) # 输入各个主成分的解释方差

loadings(fit) # 输入载荷

plot(fit,type="lines") # 碎石图

biplot(fit) # 对前两个主成分绘图

从下面的*幅图来看，前两个主成分的累计方差贡献率到达95.8%，并且碎石图的结果也显示前两个主成分所占方差较大，因此我们其实只需用这两个主成分就能很好描画鸢尾花的特征了。

各个主成分的载荷实践上反响的是各原始变量和主成分的关系，从图中结果我们不美观出，主成分1主要反映花萼长度、花瓣的长度和花瓣的宽度这三个原始变量，而主成分2主要反映花萼宽度这个原始变量，因此前两个主成分基本就能完全反映一切的变量特征了。

*后一幅图实践上是依照前两个主成分绘制的散点图，从图中不美观出：应用主成分1可以将“setosa”与其他两类分开，然后应用主成分2将“versicolor“和”virginica“分开。

这里我想和大家引见一下“psych“包（一个十分弱小的统计R包）的主成分函数principal( )，这个函数可以协助我们提取和旋转主成分：

# 极小气差旋转法
# 保管前两个主成分
library(psych)
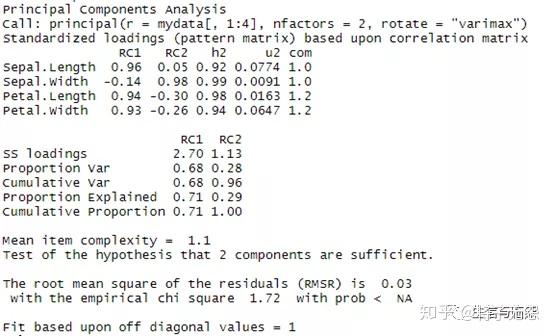
fit2 <- principal(mydata[,1:4], nfactors=2,rotate="varimax") #nfactors指定主成分个数，rotate指定旋转方法
fit2 # 输入结果

关于rotate参数，我们主要有如下选项 "none", "varimax", "quatimax","promax", "oblimin", "simplimax"和"cluster"，有兴味的冤家可以自行了解，我在这儿就不赘述了。

从上图的结果来看，前两个主成分的累计方差贡献率为96%，并且*主成分主要表征花萼长度、花瓣的长度和花瓣的宽度这三个原始变量，而第二主成分主要反映花萼宽度这个原始变量，这和之前的剖析分歧。

2. 主成分回归

接上去，我将以fit2的结果为例引见本期内容*重要的局部---主成分回归：

# 提取主成分
detach(mydata) # 解固定原数据
PC <- as.data.frame(fit2$scores) # 提取各观测点的主成分
PC <- cbind(PC,mydata$type) # 按列兼并
colnames(PC) <- c("PC1", "PC2","type") # 重命名变量
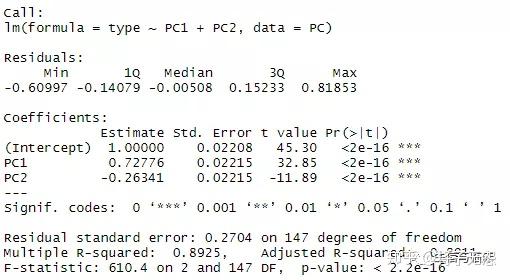
fit3 <- lm(type ~ PC1 + PC2,data=PC) # 应用前两个主成分对type停止线性回归
summary(fit3)

输入结果显示PC1和PC2都是十分清楚的，而PC1的效应量为正值，PC2则是负值，这和主成分结果分歧。

关于主成分剖析的内容就讲到这里，希望大家能掌握主成分剖析的方法以及如何用主成分停止回归剖析，我们下期再见！